Izračunavanje umnoška velikih vektora nije lak zadatak. Može zahtijevati velike izračune i vrijeme prilikom ručnog izračunavanja. Međutim, u današnjoj eri visokih računalnih alata, blagoslovljeni smo s MATLAB-om koji čini mnoge izračune u najkraćem vremenu koristeći ugrađene funkcije. Jedna takva funkcija je križ() što nam omogućuje da odredimo umnožak dvaju vektora.
Ovaj vodič će otkriti:
- Što je unakrsni proizvod?
- Zašto trebamo odrediti unakrsni umnožak?
- Kako odrediti umnožak dvaju vektora u MATLAB-u?
- Primjeri
- Zaključak
Što je unakrsni proizvod?
The rezultat dva vektora od dva vektora je fizikalna veličina koja se izračunava množenjem dva vektora. Vraća vektor okomito na data dva vektora. Ako A i B su dvije vektorske veličine, njihov unakrsni produkt C je dan kao:
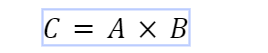
Gdje C je također vektorska veličina i okomita je na obje A i B .
Zašto trebamo odrediti unakrsni umnožak?
The rezultat dva vektora obavlja mnoge zadatke u fizici, matematici i tehnici. Neki od njih navedeni su u nastavku.
The rezultat dva vektora koristi se za pronalaženje:
- Površina trokuta.
- Kut između dva vektora.
- Jedinični vektor okomit na dva vektora.
- Površina paralelograma.
- Kolinearnost između dva vektora.
Kako implementirati umnožak dvaju vektora u MATLAB-u?
MATLAB nam olakšava s ugrađenim križ() funkcija za pronalaženje rezultat dva vektora od dva vektora. Ova funkcija prihvaća dva vektora kao obvezne ulaze i daje njihove unakrsna proizvodnja t u smislu vektorske količine.
Sintaksa
The križ() funkcija se može implementirati u MATLAB-u na sljedeće načine:
C = križ ( A,B )C = križ ( A,B,dim )
Ovdje,
Funkcija C = križ (A,B) je odgovoran za izračun križni umnožak C zadanih vektora A i B .
- Ako A i B predstavljaju vektore, moraju imati a veličina jednak 3 .
- Ako A i B predstavljaju dvije matrice ili višesmjerne nizove, moraju imati istu veličinu. U ovoj situaciji, križ() funkcija smatra A i B kao skup vektora koji ima tri elementa i izračunava njihov rezultat dva vektora duž prve dimenzije koja ima veličinu jednaku 3.
Funkcija C = križ(A,B,dim) je odgovoran za izračun križni umnožak C zadana dva niza A i B uz dimenzija dim . Imajte na umu da A i B moraju biti dva niza iste veličine i veličina (A, dim) , i veličina (B, dim) mora biti jednako 3 . Ovdje, dim je varijabla koja sadrži pozitivnu skalarnu veličinu.
Primjeri
Razmotrite neke primjere kako biste razumjeli praktičnu provedbu križ() funkcija u MATLAB-u.
Primjer 1: Kako odrediti umnožak dvaju vektora?
U ovom primjeru izračunavamo unakrsni proizvod C zadanih vektora i pomoću križ() funkcija.
A = [ - 7 9 2.78 ] ;B = [ 1 0 - 7 ] ;
C = križ ( A,B )

Sada možemo potvrditi naš rezultat C uzimajući svoje točkasti proizvod s vektorima A i B. Ako C je okomito na oba vektora A i B to implicira C je rezultat dva vektora od A i B . Možemo provjeriti okomitost od C s A i B uzimajući svoje točkasti proizvod s A i B . Ako je točkasti proizvod od C s A i B jednaki 0. to implicira C je okomito do A i B .
točka ( C,A ) == 0 && točka ( C, B ) == 0Nakon izvršenja navedenog ispitivanje okomitosti, dobili smo a logička vrijednost 1 to implicira da je gornja operacija istinita. Stoga zaključujemo da rezultantni vektor C predstavlja rezultat dva vektora zadanih vektora A i B .

Primjer 2: Kako odrediti umnožak dviju matrica?
Navedeni primjer izračunava unakrsni proizvod C zadanih matrica A, stvoren pomoću funkcije magic() i B , matrica slučajnih brojeva, koristeći križ() funkcija. Obje matrice A i B jednake su veličine.
A = magija ( 3 ) ;B = rand ( 3 , 3 ) ;
C = križ ( A,B )
Kao rezultat, dobivamo a 3-na-3 matrica C to je rezultat dva vektora od A i B . Svaki stupac od C predstavlja rezultat dva vektora odgovarajućih stupaca A i B . Na primjer, C(:,1) je rezultat dva vektora od A(:,1) i B(:,1) .

Primjer 3: Kako pronaći umnožak dvaju višesmjernih nizova?
Dani MATLAB kod određuje unakrsni proizvod C zadanih višesmjernih nizova A , niz nasumičnih cijelih brojeva i B , niz nasumičnih brojeva, koristeći križ() funkcija. Oba niza A i B jednake su veličine.
A = randovi ( 100 , 3 , 4 , 2 ) ;B = randn ( 3 , 4 , 2 ) ;
C = križ ( A,B )
Kao rezultat, dobivamo a 3-na-4-na-2 niz C to je rezultat dva vektora od A i B. Svaki stupac od C predstavlja rezultat dva vektora odgovarajućih stupaca A i B . Na primjer, C(:,1,1) je umnožak od A(:,1,1) i B(:,1,1) .

Primjer 4: Kako pronaći umnožak dvaju višesmjernih nizova duž zadane dimenzije?
Razmotrite nizove A i B iz Primjer 3 imajući veličinu 3-po-3-po-3 i koristite križ() funkcija za pronalaženje njihovih rezultat dva vektora uz dimenzija dim=2 .
A = randovi ( 100 , 3 , 3 , 3 ) ;B = randn ( 3 , 3 , 3 ) ;
C = križ ( A,B, 2 )
Kao rezultat, dobivamo a 3-po-3-po-3 niz C to je rezultat dva vektora od A i B . Svaki red od C predstavlja umnožak odgovarajućih redaka A i B. Na primjer, C(1,,1) je umnožak od A(1,:,1) i B(1,:,1) .

Zaključak
Pronalaženje rezultat dva vektora od dva vektora je uobičajena operacija koja se široko koristi u matematičkim i inženjerskim zadacima. Ova se operacija može izvesti u MATLAB-u pomoću ugrađenog križ() funkcija. Ovaj vodič objasnio je različite načine implementacije rezultat dva vektora u MATLAB-u koristeći više primjera.